Correspondencia Cinemática un marco de contacto suave para impactos deformables

Convirtiendo los impactos en ecuaciones que se comportan

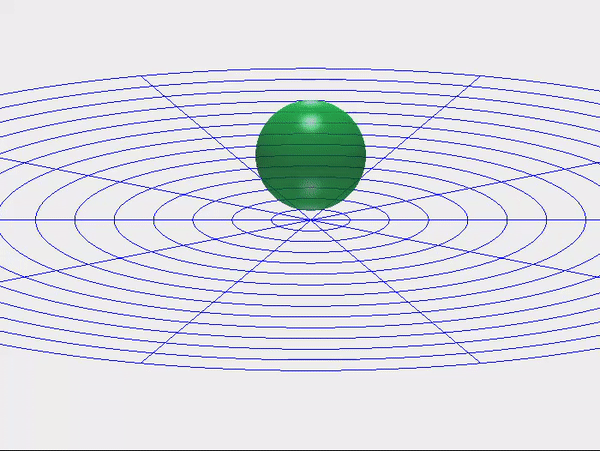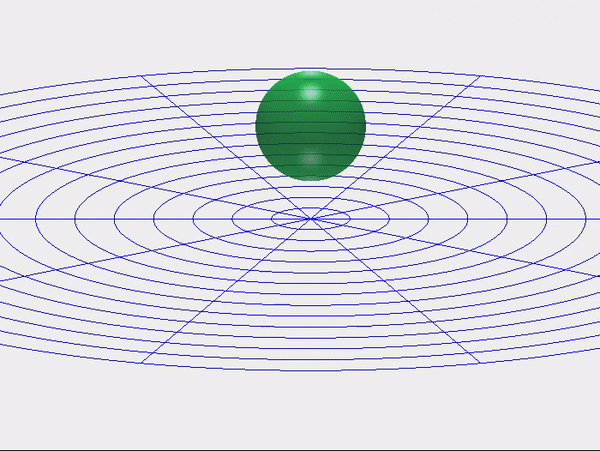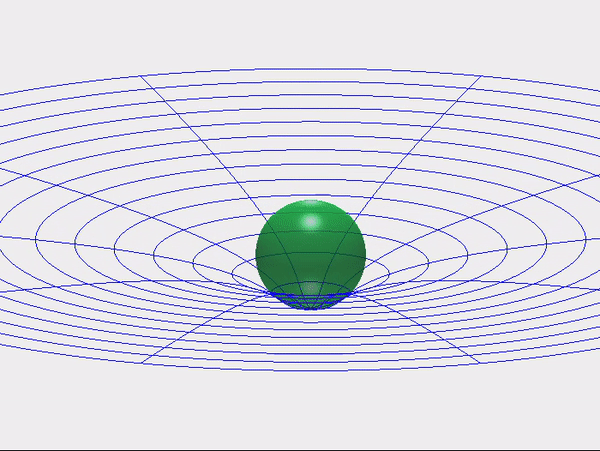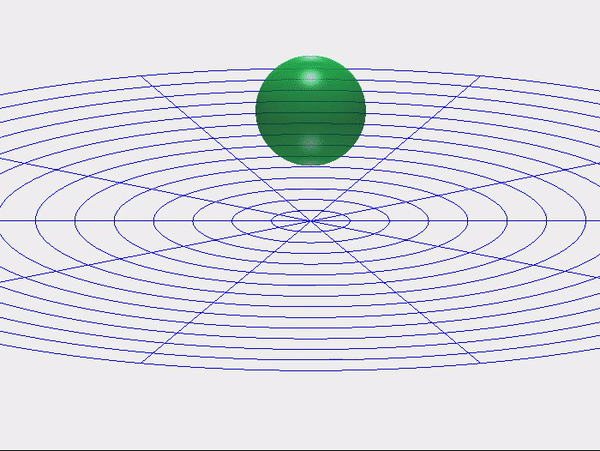
Las colisiones entre cuerpos blandos o deformables son engañosamente difíciles de computar. A medida que dos superficies se encuentran, su geometría cambia más rápido de lo que el solucionador puede rastrear, y la mayoría de los modelos de contacto manejan esto insertando fuerzas de penalización rígidas o conmutaciones discontinuas entre “tocar” y “separar”. Estos atajos hacen que las simulaciones sean inestables, demasiado sensibles a la resolución de la malla e indiferentes a la transferencia de energía real.

El marco de Correspondencia Cinemática (KM) reemplaza estas reglas ad hoc con una única condición geométrica: el ángulo de incidencia entre las superficies en contacto debe evolucionar suavemente. Esto transforma el impacto de un evento discontinuo en una restricción bien planteada y diferenciable, una que los solucionadores clásicos pueden aplicar directamente.

Por qué es importante

KM proporciona una forma estable de simular colisiones deformables y rebotes: problemas que abarcan desde la robótica blanda hasta el impacto de gotas y la acreción planetaria. En lugar de forzar el contacto a través de parámetros empíricos, KM lo trata como una condición de compatibilidad entre superficies, asegurando un “apretón de manos” continuo a medida que se acercan, comprimen y separan. Este enfoque produce:

• Disipación de energía predecible sin necesidad de ajustar constantes.
• Convergencia estable con mallas burdas.
• Compatibilidad directa con la optimización y la inferencia basada en adjuntos.

El método en un párrafo

KM aumenta las ecuaciones que rigen el sistema con una restricción suave del ángulo de contacto definida a lo largo de la interfaz. En forma discreta, acopla la curvatura y los vectores normales entre las dos superficies en contacto, obligándolas a alinearse suavemente en el tiempo. El resultado es una variedad de contacto continuamente diferenciable (sin irregularidades ni discontinuidades), lo que permite una integración estable a través del impacto, el rebote y la separación. El método se puede implementar en esquemas de diferencias finitas, elementos finitos o de captura de interfaz con cambios mínimos en las bases de código existentes.

Evidencia de experimentos y simulaciones

• Sólido-sólido: En Proceedings of the Royal Society A ((Agüero et al., 2022)), validamos KM simulando una esfera rígida que golpea una membrana elástica. El método capturó no solo los perfiles de deformación, sino también las tasas de transferencia de energía observadas experimentalmente.
• Fluido-estructura: En Journal of Fluid Mechanics ((Gabbard et al., 2025)), KM se extendió a gotas que rebotan en baños de fluido, reproduciendo con precisión las ondas capilares y los umbrales de coalescencia, regímenes en los que la CFD convencional falla.

Por qué es eficiente y general

Debido a que KM expresa el contacto a través de la geometría en lugar de las fuerzas de penalización:

• Mejora el acondicionamiento de los sistemas lineales en el momento del impacto.
• Elimina la necesidad de un remallado localizado cerca de la interfaz.
• Funciona en todos los materiales y escalas, desde la robótica blanda hasta los impactos granulares.
• Sigue siendo diferenciable, por lo que es compatible con el diseño basado en gradientes, la inferencia de parámetros y los flujos de trabajo de optimización bayesiana.

Qué sigue

Estamos extendiendo KM a sistemas multimateriales e inspirados en la biología, donde las interfaces pueden crecer, fusionarse o desgarrarse. La estructura de restricción diferenciable también abre la puerta a sustitutos de aprendizaje automático que aprenden la dinámica del impacto a partir de datos de simulación, lo que acelera las tareas de diseño en robótica y ciencia de los materiales.

Las colisiones no son eventos discretos, son conversaciones entre geometrías. Kinematic Match le da a ese diálogo una forma matemática precisa: suave, estable y computable.