Spin transport by measurement and inference

Quantifying spin transport with model-based experiments

Modern devices run into thermal and quantum limits. Spintronics routes information through spin currents rather than charge alone, promising lower dissipation. This project measured and inferred spin-transport properties in thin FM/NM bilayers using a pipeline that links the Landau–Lifshitz–Gilbert (LLG) model, ferromagnetic resonance (FMR) spectroscopy, and the inverse spin Hall effect (iSHE). The work spans sample fabrication to signal processing and ties each decision to a computable quantity: the Gilbert damping ( \alpha ) and an iSHE voltage proxy for spin current. :contentReference[oaicite:1]{index=1}

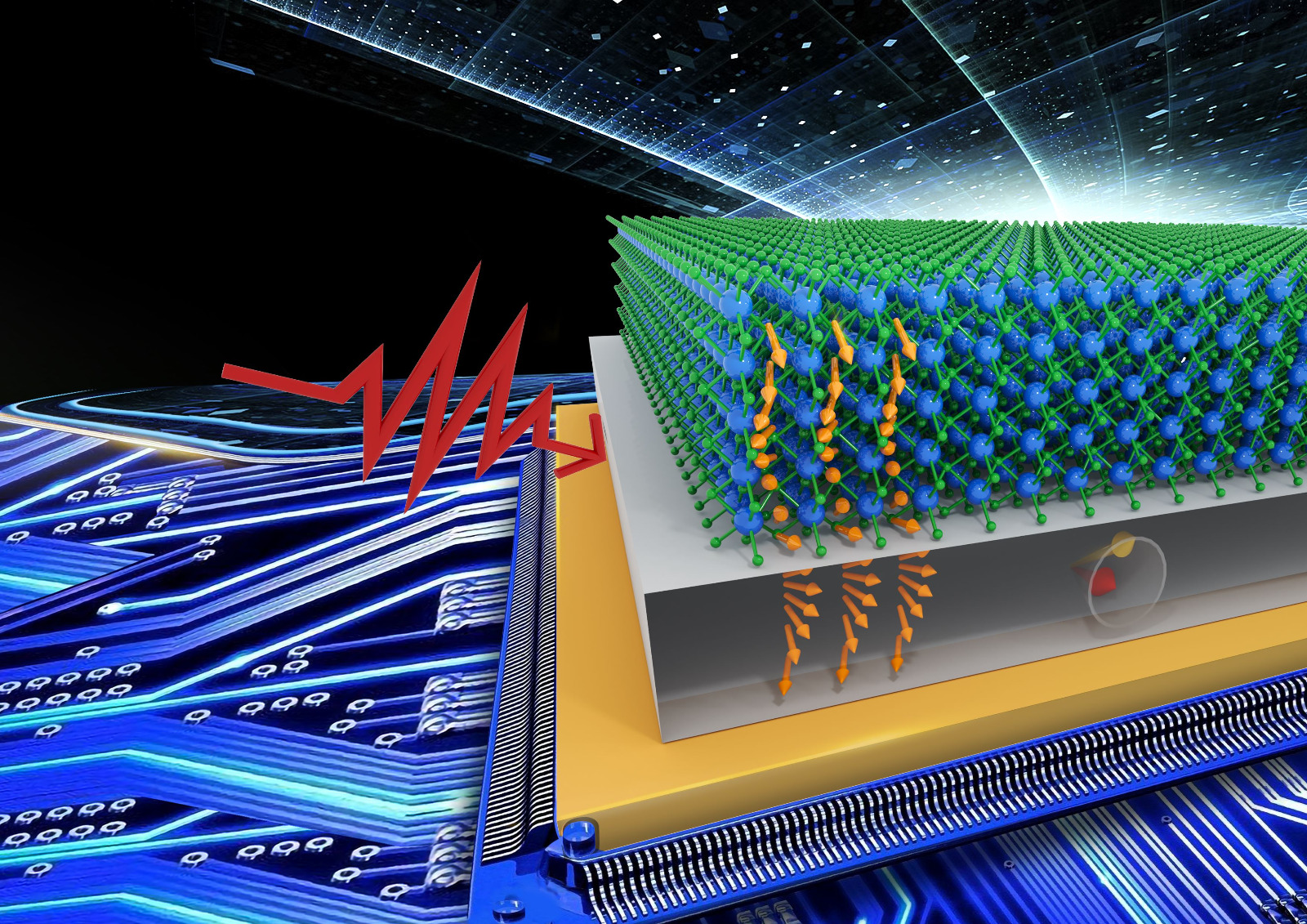
What we measured and why it’s hard

• LLG → FMR linewidth: Using LLG, the FMR linewidth–frequency slope gives the damping ( \alpha ). Clean estimates require lock-in detection, line-shape modeling, and careful anisotropy handling. We built a frequency-swept FMR pipeline and fit symmetric/antisymmetric Lorentzians to extract ( \Delta H ), ( H_{\mathrm{res}} ), and ( \alpha ). :contentReference[oaicite:2]{index=2}
• iSHE voltage under confounders: iSHE signals are small and often contaminated by AMR. We measured iSHE with intensity modulation and used a reference stack (Py/Ti) to isolate the antisymmetric AMR component, then subtracted it from Py/Pt (and Py/W) to recover the symmetric iSHE contribution. :contentReference[oaicite:3]{index=3}

Experimental design to inference chain

1. Fabrication and calibration: Sputtered Py(30 nm)/NM(6 nm) stacks (NM ∈ {Pt, W, Cu, Ti}); verified thickness and roughness with XRR; used XPS to diagnose oxidation in Py. :contentReference[oaicite:4]{index=4}
2. FMR spectroscopy: Lock-in detection with field modulation; fit derivative-Lorentzian line shapes to obtain linewidth vs. frequency → linear slope → ( \alpha ) per stack. :contentReference[oaicite:5]{index=5}
3. Materials signal: Observed larger damping enhancement with higher atomic number NM (Pt, W), consistent with stronger spin–orbit coupling; controlled for Py oxidation by using Ti as a weakly perturbing cap and by switching to YIG (insulating FM) to eliminate AMR leakage. YIG/Pt produced the cleanest iSHE. :contentReference[oaicite:6]{index=6}
4. iSHE deconvolution: Computed iSHE by subtracting the AMR-dominated Py/Ti trace from Py/Pt and Py/W; for YIG/NM, the iSHE line is directly Lorentzian with opposite signs for Pt vs W, matching spin–orbit sign expectations. :contentReference[oaicite:7]{index=7}

Results (decision-relevant)

• Ranking for spin current injection: Pt > W ≫ Cu, Ti in both damping enhancement and iSHE amplitude; YIG/Pt is the most robust pair due to the insulating FM and strong spin–orbit NM. :contentReference[oaicite:8]{index=8}
• Confounder control: Py oxidation biases ( \alpha ); established a practical correction strategy (cap-layer control + XPS confirmation) and a cleaner baseline with YIG. :contentReference[oaicite:9]{index=9}
• Signal separation: AMR/iSHE disentanglement via reference-stack subtraction yields stable iSHE estimates even at low SNR. :contentReference[oaicite:10]{index=10}

Why this matters beyond spintronics

This is a general measure-and-infer template under noise and confounding:

• Start from a governing model (LLG), design an experiment that yields identifiable parameters, and build a fitting procedure with explicit nuisance separation (AMR vs iSHE).
• Validate materials hypotheses using orthogonal probes (XRR, XPS) and a reference/control stack.
• Treat the lab as a data system: we also built a low-cost IoT monitor (ESP8266 + Hall flow sensor) to protect FMR uptime with automated email alerts. :contentReference[oaicite:11]{index=11}

Methods & data: Full report (PDF)
Core skills: model-based experimental design, line-shape fitting, lock-in detection, uncertainty handling, thin-film fabrication and validation, reference-based deconvolution, and practical instrumentation. :contentReference[oaicite:12]{index=12}